Impermanent loss (IL) is like an exogenous tax on the suppliers in automated market makers (AMMs). While liquidity providers (LPs) can hedge their IL, this tactic merely reduces its variance. Worst of all, it exceeds the fee revenue in most AMMs, which is not a long-run equilibrium. Fortunately, there is a straightforward way to significantly reduce the IL while maintaining the autonomy of these algorithmic trading contracts. A contract with the functionality described below is on the Goerli testnet and can be accessed here (its verified code is revealed here). I gave away my previous musing on extending Uniswap’s AMM to handle perps and stablecoins, but this one is copyrighted and has a patent pending.
The key to removing IL is having the liquidity providers (LPs) dominate price-discovery trades on their pools. In practice, an AMM’s arbitrageurs are not the LPs, and we commonly model the IL assuming the LP passively leaves his position alone or hedges on Binance. However, if the LP collective drives the net price changes on their pools, its net position is unaffected, as the change in the LP position mirrors the price-setting trades. If the LP’s net position does not change, it avoids adverse selection, and its IL is zero.
The simplest case
Consider a constant product AMM where Bob is the only LP and its only trader. I will use the leveraged AMM I described earlier here. In this AMM, traders and LPs can leverage their positions, and when they do so, the borrowed tokens are debited from their ETH or USD accounts. This nets an LP’s pool positions with subsequent trades, generating a cross-margining effect. Further, this lowers the operational risk created by having to transact on different platforms, often off the Ethereum main chain.
Assume LP Bob is levered at 20:1, so the pool tokens implied by Uniswap v2 math are 20 times greater than his actual token amounts invested. While this approach generates an unrestricted range, leverage enables it to be as capital efficient as a Uniswap v3 restricted range pool; 20:1 leverage is about what one gets with a v3 range with price bounds +/- 10% from the current price. For example, Bob adds 1.0 ETH to become an LP in this LAMM, and the current ETH price is 1296 USD. There is 20x leverage for LPs, so his pool ETH is 20.
With 20x LP leverage, this implies liquidity of 720 via
- poolETH = liquidity /sqrt(price)
- sqrt(1296)= 36
- poolETH = 20
- liquidity = 20*36 = 720
Given this liquidity, we calculate the pool USD
- PoolUSD = liquidity * sqrt(price) = 720 * 36 = 25,920
With poolUSD of 25,920 and 20x leverage, he will need to deposit 1,296 in USD.His trading accounts will reflect his initial ETH and USD deposits and the borrowed amounts in his pool positions.
- Initial trade account ETH = ETH deposit – poolETHborrowed = 1 – 20 = – 19
- trade account USD = USD deposit – poolUSDborrowed = 1,296 – 25,920 = – 24,624
LP Bob’s net ETH position is 1.0, his initial ETH deposit. This is the sum of his pool ETH and trade account ETH. His liquidity number and the square root of price imply his pool positions, so these change as the AMM’s price changes. Bob’s subsequent trades are credited and debited in his trade accounts.
- pool ETH = liquidity/sqrt(price)
- trade account ETH = initial ETH deposit – initial poolETH + subsequent trades
- pool USD = liquidity*sqrt(price)
- trade account USD = initial USD deposit – initial poolUSD + subsequent trades
- Net tokens = pool tokens + trade account tokens
In Figure 1 below, all price movements are caused by Bob’s trades that are added to his trade account, where his ETH purchases reduce his ETH debt. These increases are precisely offset by declines in the contract’s pool ETH position, which in this case means Bob’s pool ETH position, leaving Bob’s net ETH position unchanged. With his net ETH and USD positions unchanged, his IL is zero. Intuitively this should make sense because he cannot lose money trading with himself, regardless of the algorithm.
Figure 1

Arbitrage Trading and Price Discovery
Price discovery happens on the cheapest and lowest latency exchanges. If you know the price of ETH is going up, your best strategy for capturing this price movement would be to buy on a low-latency exchange first and then send an order to a blockchain AMM. Sending trades to a blockchain AMM and a centralized exchange simultaneously would generate the same result, as the blockchain trade would appear at least ten seconds after your Binance trade went through. It would make no sense to send a large buy on the blockchain first and then send a large buy order to Binance after it gets processed because that would only allow others to front-run your second trade.
Many people think that since there is so much volume on Uniswap, it is likely that ETH price discovery is happening on these blockchain AMMs. If Uniswap had comparable latency, this would make sense, but the latency difference is 100-fold at minimum. If we remember that way back in 2009, firms spent $300 million building a more direct cable from Chicago to New York to save four milliseconds; even the centralized blockchains like Solana are orders of magnitude slower than standard centralized exchanges.
Ultimately, this is an empirical issue. Figure 2 below shows that 80% of the time, Uniswap prices are within Gemini prices by 0.1%. More importantly, for my argument, we see that when the Uniswap price diverges from the Gemini price, the Uniswap price moves towards the Gemini price and not vice versa.
Figure 2
Uniswap 0.05% ETH/USDC Pool
Gemini/Pool premium vs. Future Gemini & Pool Price Changes
Data from the second quarter of 2022. I took the Gemini minute-downsampled prices, paired them with the next Uniswap price, and then looked at the price 3 minutes later.

To give LPs an arbitrage-trader advantage, we let LPs trade for free on the contract, while everyone else would have to pay a fee, such as 0.2%. Traders paying the fee need the AMM’s price to deviate by 0.2% from the ‘true price’ to consider an arbitrage trade, while the LP is incented to arbitrage trade well below that level (above unlisted costs like those from gas). If LPs traded each time the Binance/Gemini price deviated by 0.2% from the AMM, the non-LP traders would never see an arbitrage opportunity and be relegated to liquidity trading.
An efficient exchange needs arbitrage traders setting prices. The LP should not pay arbitrageurs anything in AMMs because price discovery for latent exchanges is not subtle: arb the AMM with Binance/Gemini prices. Non-LP arbitrage profits add a significant cost to an essential party in the exchange, a cost that must eventually get charged to liquidity traders in a sustainable AMM. When the arbitrageur and arbitragee are the same entity, this eliminates a significant deadweight cost, which is always a good thing.
A simple fee exemption would be sufficient to make this work if there was only one LP, but with multiple LPs, we need more rules to prevent some LPs from dominating arbitrage trading.
Consider the case where Bob and Alice are LPs. In figure 3 below, Bob has twice the liquidity as Alice, and Bob trades twice as much as Alice, and the result is that both end up with the same net ETH at the new price. There will be slight IL because Bob’s USD change is not exactly twice that of Alice, but this is generally insignificant (or at least second-order).
Figure 3
LPs Bob and Alice trade proportional to their liquidity
Data to the right are units of ETH

In contrast, in Figure 4 below, only one LP trades, resulting in significant net ETH position changes for both LPs. While some LPs would be averse to generating a change in their net ETH position, some would appreciate the profit as worth the risk. Without some sort of restriction, LPs with superior blockchain connectivity would dominate arbitrage trading, leaving those without bleeding-edge access susceptible to the standard IL.
Figure 4
Only One LP Trades Alice Trades

We need to add conditions to prevent low-latency LPs from dominating arbitrage. A simple rule based on the LP’s current net ETH position compared to their initial net ETH position can do this because when LPs trade proportional to their liquidity, their net ETH position is constant. Therefore the LPs can buy for free only if their net ETH position is less than 100% of their initial ETH position and can sell for free only if they have more than 100% of their initial net ETH position. This incents LPs to arbitrage price changes only when it reduces their IL, so aggressive LPs will get a ‘time out’ when they trade too much.
An LP’s net ETH position relative to her initial net ETH reflects her relative arbitrage trading, assuming she does not add or subtract ETH exogenously. To make the LP’s net ETH position reflect their relative trading, we need to restrict LPs from depositing or withdrawing ETH from their accounts while they provide liquidity, as otherwise, their net ETH position would not reflect their relative trading.
Managing LP Liquidity
In a standard constant product AMM, when the price moves the pool amounts of one of the tokens decrease. In an AMM with 20:1 leverage, the LPs would generate negative net token positions when prices move by about 10%. While traders could supply sufficient tokens for trading in the short run for this AMM to continue operating, it is not an equilibrium for a sustainable pool.
To mitigate this risk, the liquidators can remove an LP’s liquidity when they have a negative net position in either ETH or USD. This constraint will bind well before the LP becomes insolvent. An LP liquidation is comparatively benign in that it merely removes liquidity and nets the pool tokens with the ex-LP’s trade account debts, so no trades are dumped onto this market.
An LP arbitraging the pool would not need to get tokens elsewhere and deposit them into the pool to avoid liquidation. If the LPs were not arbitraging the pool, they would be forced to wrangle up tokens to deposit into the pool, which requires more capital, trading expense, and operational risk. This wrangling is avoided when they can trade on the same contract where they provide liquidity. Ideally, the LPs trade proportionate to their liquidity and never need to rebalance their pool using outside tokens.
A hack to this system would be for a ‘just in time’ liquidity provision and trade. Carlos could add liquidity, make a trade, then remove liquidity, all in one block. Such transactions are parasitic and need to be discouraged. Therefore we penalize LPs who remove liquidity within a week, so anyone just wishing to trade will find the tactic of ‘add liquidity/trade/remove liquidity’ unattractive.
Liquidity trader Imbalances
If the LPs generate 100% of the net trades needed to move the AMM price, the non-LP trades must be zero-sum. If there is a temporary excess demand in one direction, the LPs can handle this in two ways.
First, they can arbitrage the price premium generated by the excess net liquidity trading and accept the resulting net ETH position change. For example, excess non-LP buys push the AMM price above its true price, and an LP can sell on the AMM, generating an arbitrage profit. The downside is the LP now has a net short position relative to her initial net ETH position, which may generate an unacceptable risk.
Alternatively, the LPs can do nothing. Non-LP demand pushing the AMM price to a premium over its true price will cause the LPs to become short ETH relative to their initial ETH position, but being short an overpriced asset is not a bad situation. On average, at some point, non-LPs will arbitrage the AMM price, pushing it down, and restoring the LP position to its initial neutral condition. If, for some reason, users prefer to buy ETH with leverage on this AMM, generating a persistent price premium on the AMM, that is not so much a problem as an equilibrium. This is purely an empirical issue but easily soluble.
Active LPs
This strategy is subtly different than hedging one’s LP position. In classical option hedging, it is assumed the hedger is a price taker, and such hedging reduces risk but does not change the expected loss for a position with negative convexity. In contrast, if the hedger effectively sets the price as an informed trader, they eliminate this convexity cost. The LP fee advantage combined with the latency of blockchain AMMs allows the LPs to trade like market wizards.
If LPs are expected to arbitrage their pools, this implies access to arbitrage bots that monitor centralized exchanges and the blockchain. The LP’s informational advantage only exists within the price-premium window of the fee amount, which requires an algorithm, APIs, and web3 capabilities. They need the ability to react to 0.2% price deviations at all hours of the day. The high latency of the blockchain works to the AMM’s benefit here, as it makes it possible for an LP arb-bot to implement a simple algorithm based on centralized exchange prices.
While such a setup is straightforward, many LPs will need assistance. One solution is that someone can provide a contract that acts as a vault and manages an arbitrage bot for that vault. The capital supplier and vault owner can then split fee revenue in some mutually agreeable way. Alternatively, the contract can allow LPs to designate other accounts to make arbitrage trades on their account but not withdraw or do anything else. This would allow an LP to hire arb-bots that can seamlessly add their account to an algorithm, tapping the various LPs depending on their individual net ETH position. The arb-bot would need a fee, but as there are economies of scale in creating and running such a program, it would generate mutual gains from trade.
It should be no surprise that active traders can game passive LPs in an AMM. Over the past century, the riskless real interest rate has been less than 1%. It is not an equilibrium for passive investors to make 5%+ without risk or effort, and many pools advertise 10% or even 100% returns for passive LPs. If investors want such returns, they will either have to create an arb-bot or find an arb-bot partner, and to expect otherwise is fanciful. Over time, those with the better arb-bots will dominate. Market making has never been only about providing capital. In centralized limit order books, the market makers always post two-sided markets—a bid and ask—which are adjusted continuously. These are highly competitive markets, and every competitive market requires a significant investment of capital and time, as well as a little alpha.
The inherent latency advantage will make AMMs derivative markets for the foreseeable future. When secure L2 solutions come around with latency comparable to centralized exchanges, traditional centralized limit order books can be used.
Example Spreadsheet
The spreadsheet below shows how a sequence of random prices affects three AMM participants’ net ETH position and demand functions. There are two LPs and one non-LP. In each period, the true price changes randomly via a random walk. The LPs then generate their desired ETH trades based on the current price on the AMM, the true price, and their current net ETH position relative to their original net ETH position. The non-LP trades randomly or targets the price if the AMM deviates from the true price by more than the fee.
You can see how the mechanism works if you play around with it. I find such simple models helpful for my intuition.
Summary:
The essential rules for an IL-free AMM are as follows. They apply to a leveraged AMM so that the contract can monitor the LP’s net ETH position, given that the LP has both pool positions implied by his liquidity and a trade account reflecting trades against the aggregate pool. The trade account for an LP starts as a negative number, reflecting the ETH borrowed to go into the pool; however, the initial net position for an LP is positive.
- Standard accounts pay a fee to trade
- LP accounts qualify for a discounted fee if a trade moves the account’s net ETH position towards its net ETH position at the time of initiating a liquidity position.
- LP’s currentNetETH < LP’s initialNetETH, buy only for zero fee
- LP’s currentNetETH < LP’s initialNetETH, sell only for zero fee
- Restrictions
- LPs cannot add or withdraw tokens from their accounts while providing liquidity.
- Withdrawals less than several days after initiating liquidity position pay a fee on pool USD removed
Appendix
Impermanent Loss Significance
IL is a significant problem for AMMs, but it is commonly ignored for two reasons. First, it is not a direct cost in that it is reflected in receiving back more of the less valuable token and less of the more valuable token. A pool with initial token amounts of ETH(0) and USD(0) will change over time to ETH(t) and USD(t). The mathematics of AMMs imply ETH(t) and USD(t) are functions of the price such that if the price of ETH rises, the LP will have less ETH and more USD, and the inverse (see more on this here).
IL(t) = p(t)*(ETH(t) – ETH(0)) + (USD(t) – USD(0))
More importantly, the main reason an LP position value changes comes from the variation in the token price unrelated to IL. Note that the IL formula above highlights it is just capturing the adverse selection of an LP’s pool positions, not the total pnl. If the token quantities are constant, the IL is zero, but the position value will change dramatically due to the change in the ETH price.
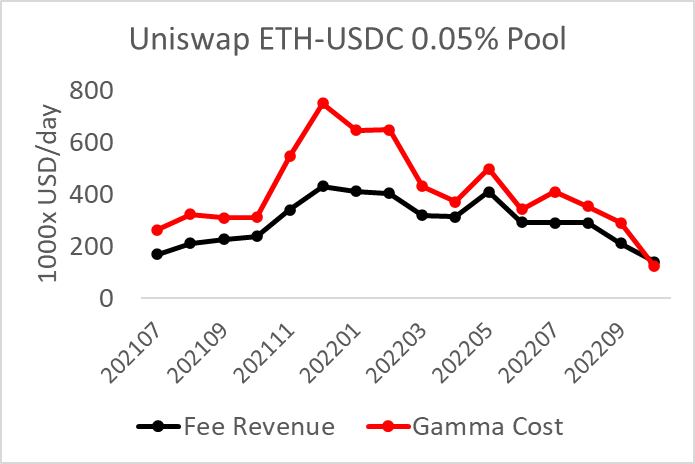
Figure 5 below shows the relative magnitudes of the total change in value for an LP vs. the IL for an unrestricted (i.e., v2) ETH/USDC pool. It is common to ignore second-order costs like these.
Figure 5
While the IL expense is relatively small, it is still significant. This is more conspicuous in the concentrated liquidity ranges offered in Uniswap v3 because a 10%+/- range uses only 5% of the capital in v2, which implies the IL becomes 20 times more prominent relative to the base price pnl changes.
If you do not calculate the loss, it is easy to ignore, and AMM promoters are not inclined to mention costs if they are not forced to. For example, a Bankless newsletter listed the top yield-farming opportunities but did not mention IL. Ribbon presents its option writing pools by listing the option premium as if it were a dividend. Uniswap’s pool portal conspicuously presents the fee revenue but nothing about the IL. When people do not mention a cost, it is no surprise they underprice it.
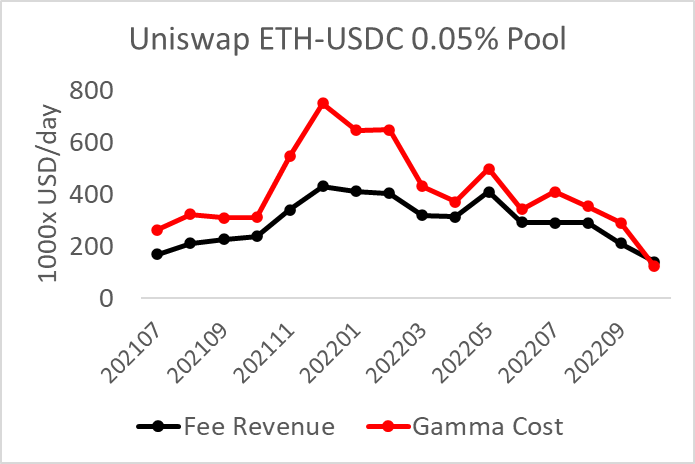
The major Uniswap pools generate ILs greater than their fee revenue, a net loss. This is easy to measure. Fee income is simple: fee times the volume traded. The IL payoff is very similar to a short straddle, which has negative convexity in that the second derivative of the LP position is negative. Specifically, we call this second derivative gamma, which for an LP position is defined as

Options theory tells us that the convexity cost is the price variance divided by two times gamma. This cost over time is called theta, which represents the expected option decay needed to offset the option seller’s gamma.
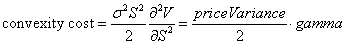
Applying this formula to Uniswap pools reveals a consistent negative pnl for LPs in that their fee income does not outweigh their convexity costs. The chart at the top of this post shows the average daily liquidity and volume for the popular ETH/USDC Uniswap v3 pool. Note it is generating a slight positive pnl this month because ETH volatility has been lower than average (data are through October 9).
A persistent systemic option underpricing has happened before. Convertible bonds are standard corporate bonds with an option, usually an out-of-the-money call with a long maturity. Before around 2005, it was common for these bonds to price their option below the price of explicit stand-alone options on stocks. These underpriced options allowed hedge funds focused on convertible bonds to generate significant Sharpe ratios for decades.
The driver of this underpricing was caused by a lack of transparency and bad incentives. The option value was rarely estimated independently, but the option value allowed the bond to have a lower explicit interest rate. If the company’s stock price fell, the option expired worthless. In that scenario, the company was clearly better off for having sold the worthless options, and management would highlight the money they saved by issuing convertible bonds. If the company’s stock price rose so that the option was in the money, shareholders were sufficiently distracted by their above-average returns that they did not criticize management.
Eventually, investment banks made it easier to isolate the options component of these bonds, and the options were priced efficiently via arbitrage. A simple convertible bond hedge fund strategy no longer generates a 1.5+ Sharpe ratio. We should expect something similar in AMMs. Currently, LPs are selling underpriced options, which creates an opportunity for those who can offer that same revenue for that service at a lower cost.
AMM Volume Not What it Appears
The net loss to LPs leads one to suspect that the impressive AMM volume is not a sign of a vibrant trading tool as it is a mechanism for savvy investors to fleece LPs who ignore their IL. As an analogy, consider the Defi exchange dYdX, which recorded a huge volume in late 2021. This was mainly driven by people taking advantage of their rewards program. Activity on their exchange was rewarded with tokens worth more than the fees generated, creating an arbitrage opportunity for throwing in some ETH and trading back and forth. Once the rewards system stopped, volume on the dYdX platform declined by over 95%.
Some believe fees from arbitrage traders generate net revenue, but this is wrong because arbitrage is purely voluntary, and they only do it to make positive profits. The arbitrageur profits are just the other side of IL. Thus the relative volume differential between the ETH/USD pools with different fees is proportional to the fee difference: six times the fee generates one-sixth the volume. The marginal trader seems to be the pool arbitrageurs, who need to make a profit to cover costs outside the pool, such as fees on centralized exchanges and capital costs (significant because they cannot be netted).