Put aside price controls for a moment and look at the figure below from their paper. Total revenue at that output is the rectangle P×Q (Area III + Area IV). Total revenue is also the integral of marginal revenue, up to the quantity purchased. The area under the MR curve is Area I + Area III. So we have a simple way to see Area I = Area IV.
Therefore, consumer surplus (which is the integral of the demand curve, minus total revenue) can be calculated in two equivalent ways, even in a competitive market:
- Traditional Method: Area I + Area II (the area between the demand curve and the price line).
- Marginal-Revenue Method: Area II + Area IV (the area between the demand curve and the marginal-revenue curve).
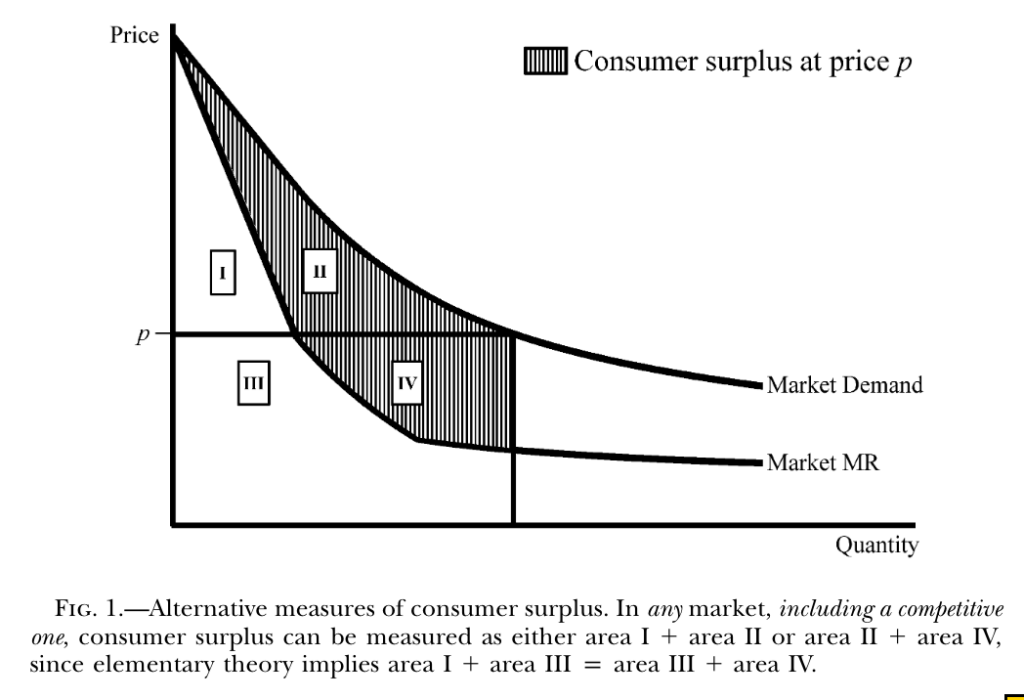
This observation might seem trivial at first, but it yields powerful results about price controls. This approach helps resolve the paradox by allowing us to cleanly analyze how misallocation and rent seeking affect welfare, even when every consumer pays a different effective price (due to queuing, search costs, etc.).
Suppose the good is allocated randomly among those willing to pay. Twenty people are willing to pay more than the rent-controlled price of $800 for an apartment. Ten apartments exist. Each has a 50% chance of getting it, regardless of whether they are willing to pay $10,000 or $801.
Using their insight, Bulow and Klemperer prove a somewhat surprising result: The misallocation effect alone can ensure that a price control always reduces consumer surplus in a competitive market with convex demand whenever supply is more elastic than demand; and even if supply is completely inelastic, a price control will reduce consumer surplus if demand is “log-convex” (such as constant-elasticity demand). That’s a mouthful, so let’s unpack the intuition.
“Supply more elastic than demand” means producers are relatively flexible in cutting back quantity when price falls, whereas consumers aren’t drastically increasing quantity demanded. In rent control, this could describe a long-run scenario: landlords (supply) can convert or repurpose housing (reducing rental supply) fairly easily, while renters (demand) desperately want housing and don’t dramatically change how much housing they need when rent drops. So, supply shrinks a lot relative to the extra quantity consumers demand at lower prices. The result is a big shortage. This is the usual shortage effect dominating.
But let’s think about the case when supply is fixed. There won’t be any shortage. But consumer welfare is still destroyed if people who value the good relatively less get the good.
Before we get to the mouth-twister about “demand log-convex,” it helps to picture what happens when demand is exactly unit-elastic over some range—that is, every 1 % drop in price raises quantity sold by 1 %. This is the blue demand curve below. (I’m not worried about the people on the far left side.) The green area is the consumer surplus.
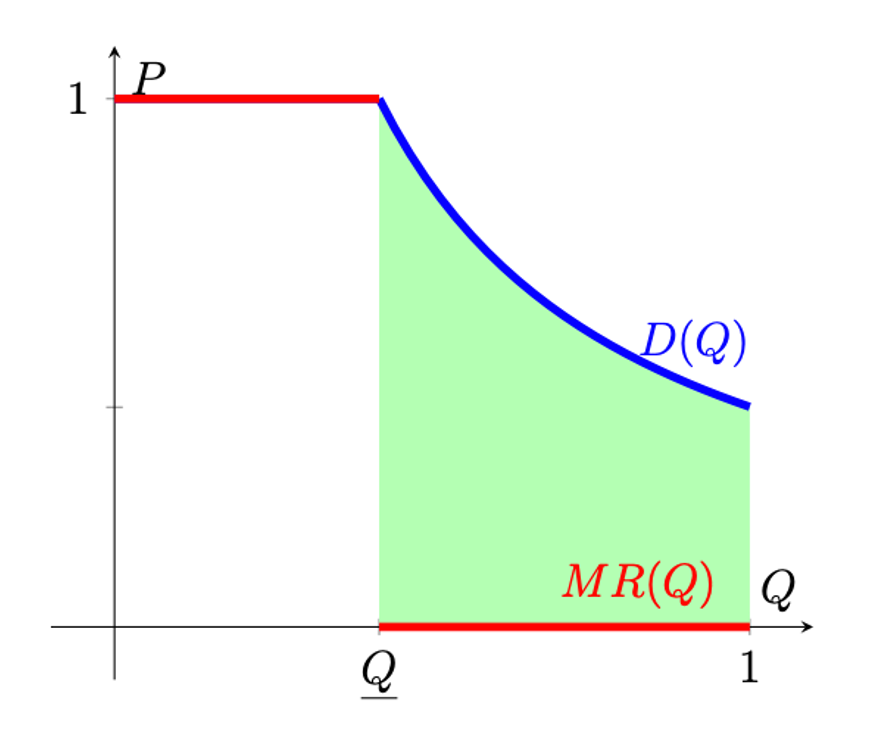
In that special case, the marginal-revenue curve lies flat at zero, as sketched in the little green-shaded diagram you just looked at. The (blue) demand curve lies above it, but MR never changes with quantity. Why is that a big deal? Remember Bulow and Klemperer’s trick: consumer surplus is the area between demand and MR. When MR hugs the horizontal axis, that wedge is huge—every slice of quantity adds almost the full height of the demand curve to consumer surplus. For intuition, this is a huge consumer surplus if you could drive down price and increase quantity.
Here’s the part that’s easy to miss. Unit-elastic demand makes the “price-cut rectangle” look gigantic because MR is sitting at zero. Every $1 you knock off the rent seems to flow straight into consumer surplus. That rosy picture would be right if the same renters stayed put.
But with a cap, who gets the apartment changes. Picture a $10,000-valuation renter iced out by the lottery, replaced by someone who values the place at $801. The market just lost almost $10,000 of surplus and gained back only $801. Because the MR gap is so tall, even a handful of high-to-low swaps wipes out more value than the lower rent ever created. In Bulow-and-Klemperer language, the dotted Y gain is swamped by the shaded Z loss—the giant MR wedge amplifies both, and the bad swap wins. So yes, the rectangle is huge, but the misallocation rectangle is even bigger.
Put differently, when the cap reshuffles apartments randomly, the newcomers value them far less than the high-valuation renters who are pushed out. That swap alone can erase more surplus than the lower price creates. So, even with perfectly fixed supply, consumer surplus falls. The convexity puts the dividing line on which effect dominates.
Rent Seeking Doesn’t Change the Key Result
Having established that price controls can hurt consumers through misallocation, let’s consider a natural question: What if high-value consumers could somehow increase their chances of getting the good through extra effort? This is precisely what happens in the real world—consumers engage in various activities to improve their odds when goods are scarce and prices are controlled.
Bulow and Klemperer’s insight is that these rent-seeking activities—standing in line, paying bribes, searching intensively for apartments, or offering side payments—don’t fundamentally alter their conclusions about when price controls harm consumers.
When consumers engage in rent seeking, they’re essentially paying a nonmonetary price on top of the official price. From a consumer’s perspective, rent-seeking costs are just another form of payment, effectively raising their total price above the controlled level.
Though rent seeking leads to a more efficient allocation than pure random rationing (because higher-value consumers typically spend more effort to get the good), the efficiency gains come at a cost. The brilliant insight is that these costs precisely offset the allocation improvement. As Bulow and Klemperer demonstrate, the economic value is fully dissipated in the competitive process of seeking the scarce goods.
The traditional way to calculate consumer surplus—the area between the demand curve and the price line—becomes problematic when different consumers pay different effective prices due to varying rent-seeking costs. This is where Bulow and Klemperer’s marginal-revenue approach proves invaluable. Their method shows that consumer surplus equals the area between the demand curve and the marginal-revenue curve, regardless of the allocation mechanism, whether it’s:
- Random allocation;
- Rent-seeking-based allocation;
- Partial decontrol; or
- Any combination of these.
Rent seeking produces a remarkable cancellation effect in the market. If all consumers had identical rent-seeking abilities, the available supply would be efficiently allocated to the highest-value consumers, just as in an uncontrolled market. The entire price reduction would, however, be eaten up by rent-seeking costs, leaving total consumer surplus unchanged. Add in any supply response (which always reduces consumer surplus), and consumers become strictly worse off than they would be without price controls.
This is why Bulow and Klemperer can make such a clear claim: under the conditions they specify (log-convex demand, or supply more elastic than demand), consumers are guaranteed to lose from price controls even with rent seeking. The presence of rent seeking doesn’t save consumers from the harm of price controls; it merely changes the mechanism through which that harm occurs.
In short, rent seeking transforms what would have been a pure misallocation loss into a combination of better allocation but added competition costs. The total effect leaves consumers in the same position with fixed supply, or in a worse position when supply responds to the lower prices. This is exactly as we’d expect from basic economics, but now proven with mathematical precision.
Price controls present an economic paradox that challenges intuitive thinking. While the immediate benefit of lower prices appears obvious, Bulow and Klemperer’s analysis reveals the exact way that the hidden costs often outweigh these benefits. Through reduced supply, misallocation of goods, and wasteful rent seeking, price controls can harm the very consumers they aim to help.
Their clever approach demonstrates that under common market conditions—elastic supply or log-convex demand—consumer welfare declines even without accounting for supply reductions. When rent seeking is factored in, the results remain unchanged: the improvement in allocation is precisely offset by the resources wasted in competition for scarce goods.
Empirical evidence backs up this misallocation effect: San Francisco’s rent-control regime meant existing tenants were more likely to stay in their apartments. Landlords responded by converting rentals to condos or other uses, reducing the rental supply by 15%. In the long run, citywide rents actually rose as the housing shortage worsened.
So, yes. Economists are correct to be down on price controls.